上一节介绍了,我们采集的信号,实际上包含了各种各样的子信号,实际情况中,这些字信号非常复杂,我们在时域看不出来都有哪些频率成分,这时候傅里叶变换就排上用场了。
傅里叶变换的提出让人们看问题的角度从时域变成了频域,多了一个维度。快速傅里叶变换算法的提出普及了傅里叶变换在工程领域的应用,在科学计算和数字信号处理等领域,FFT至今依然是非常强大的工具之一。傅里叶变换的物理意义是把时域复杂的信号在频谱中分解出来,时域无法确定信号有哪些频率,但是在频域上看就非常清晰。
图3-4 是用Matlab实现FFT的关键代码,x为原始信号,n为原始信号长度,输出y为FFT后单边频谱,f为频率。

图3-4 Matlab实现FFT
比如图3-5 中的复杂信号y,y=0.1+0.9*sin(2π*25*t)+0.4*sin(2π*250*t)+0.46*sin(2π*412*t),在第一行的时域就难区分出这三种频率,直接看时域的信号波形,我们是看不出来这个信号是由哪些信号组合来的
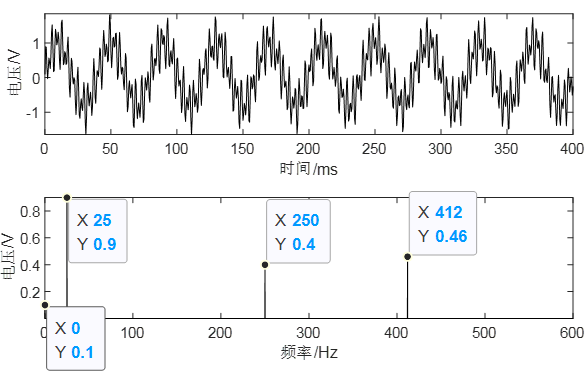
图3-5 复杂信号的时域与频域
但是经过傅里叶变换以后,在频域看,就非常清晰了,三种信号频率以及幅值跃然纸上,图3-5 第二行可以看到3条频率谱线,分别是0.9v@25Hz、0.4V@250Hz、0.46V@412Hz ,还有一个0.1V的直流成分,那么我们就可以通过频域轻松知道这个y的组成了:y= 0.1+0.9*sin(2*pi*25*t)+0.4*sin(2*pi*250*t)+0.46*sin(2*pi*412*t)(本节不讨论相位信息)。如果只从时域来分析的话就非常难了,FFT极大的加快了我们分析信号的效率。
-END-
我是工程师看海,脑机接口高级顾问,《运放秘籍》原创者,带大家一起畅游科技之海,任何卡点可1V1解答。
更多内容在《运放秘籍》第三部:信号、电路与系统新说
