
在本文中,我们将研究一个由二极管和RC电路组成的简单电路,该电路能够揭示微波脉冲的射频包络。
方波调制
假设我们有一个正弦振荡,它被一个方波截断并进行幅度调制:

其中:

这里,n是一个非零自然整数,它决定了振荡次数,从而决定了信号v(t)的持续时间,由τ0=nT0给出,其中T0=1/f0。而Tp>T0的时刻,则是方波vq(t)的周期。
在图1中,我们报告了n=1和f0值递增时v(t)的行为。在这里我们看到,在[0,τ0]内,信号只进行一次振荡。
但需要注意的是,n不能任意大:如果n=Tpf0,则v(t)为零的区间[nT0,Tp]退化为点{Tp}。更准确地说,n取值的集合的上界为N=[Tpf0],其中[·]表示整数部分。
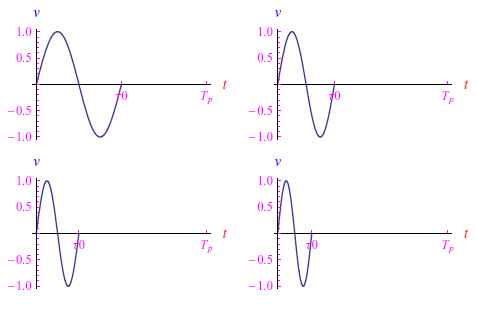
图1:当n=1、Tp=1s且f0=2、3、4、5Hz时的信号趋势(1)。无论f0的值如何,信号在τ0设定的时间范围内都只进行一次振荡。
在Wolfram语言中,上述参数可以通过Piecewise指令轻松实现。Piecewise函数(公式(1))的参数除了自变量t之外,还包括频率f₀、周期Tₚ和自然整数n。图1中的图形是使用GraphicsArray指令绘制的,展示了在将Plot指令定义为n的函数后,上述函数的变化趋势。
总体而言,我们观察到如图2所示的趋势。雷达脉冲的传输采用方波调制。图3展示了一个典型的波列,该波列由一个周期为1ms的方波调制的微波脉冲(f₀=9GHz,脉冲宽度1µs)组成。图中还显示了返回的回波。
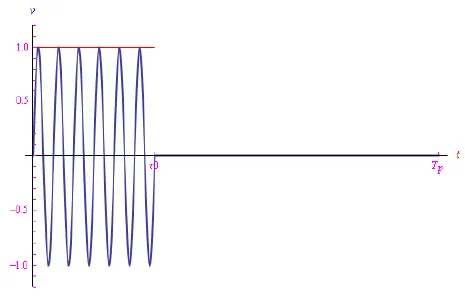
图2:信号(1)由方波(2)进行幅度调制
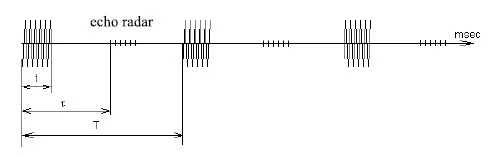
图3:由射频方波调制的典型雷达脉冲
包络检波器
在雷达技术中,关键在于调制脉冲的方波(图3)。从数学角度来看,该分量可通过将公式(1)的第一项和第二项除以sin(2πf₀t)得到。从电子角度来看,使用一个在阴极输出端负载的检波二极管,并连接一个RC电路,该组件可在输出端输出不含射频成分的脉冲波。由此,我们得到了图4所示的电路图。
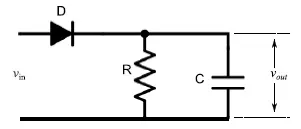
图4:包络检波器
从对低频信号幅度调制情况下的包络检波器的讨论可知,与输入(1)对应的输出信号vout(t)是以下柯西问题的未知函数x(t)(已在之前讨论过):
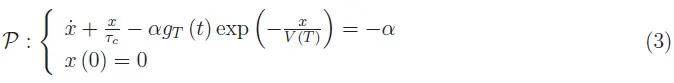
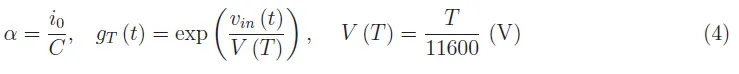
其中:i0为二极管的反向饱和电流;τc=RC为RC电路的时间常数;T为二极管的工作温度;vin(t)为由式(1)给出的输入信号。我们感兴趣的是式(3)在区间[0,Tp]内的解。根据柯西-利普希茨定理,问题(3)在上述区间内有且仅有一个解。该微分方程是一阶的、非线性的、非齐次的,其中vin(t)是一个非恒等零函数。反之:
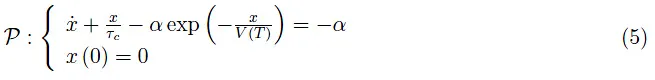
该方程仅存在平凡解。这正是我们所预期的,因为此时未施加输入信号。然而,我们观察到,如果x(0)=x₀≠0,即使在没有信号的情况下,我们仍然有一个非零解x(t)。从物理角度来看,这是因为电容器初始时是带电的(因此其两端存在电势差)。
在室温(300K)下,V0=V(300)=2.59·10V。因此:
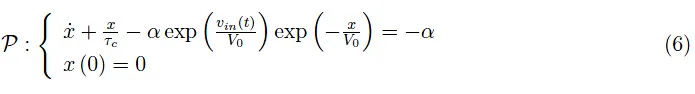
假设:R=10MΩ,C=10⁻¹µF,i=1µA。一个典型的由射频方波调制的微波脉冲具有以下特征:
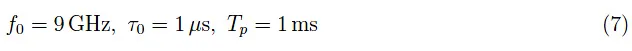
遗憾的是,Tp值远大于τ0,这使得我们无法绘制输入信号的图像,因此也无法得到柯西问题(6)的相应解。那么,让我们假设一个输入信号频率为:
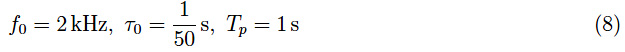
图5显示了该解的图形,而图6则展示了[0,T——/10]范围内的解,从中我们可以识别出二极管截止范围内的电容器放电过程。

图5:输入信号由公式(8)表征时,解在[0,Tp]区间内的变化趋势。输入信号以虚线表示。
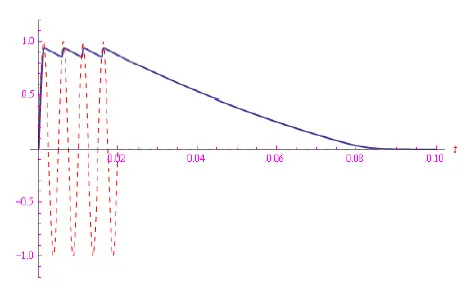
图6:输入信号由方程(8)表征时,解在[0,Tp/10]范围内的变化趋势
结果令人失望,因为即使在方波的衰减阶段仍然存在信号。这是由于电容器的电容值相对较高,因此需要更长时间才能通过电阻器放电。实际上,可以用变容二极管代替电容器,众所周知,变容二极管可以仿真电容器,其电容值取决于施加的电压。
然而,这种配置较为复杂,因为变容二极管采用反向偏置。理想情况下,我们仍然可以将其视为随施加电压变化的可变电容;具体而言,当方波处于峰值时,电容C取恒定值C1,而当方波衰减时,电容C取恒定值C2 <C1。例如,当C1=10< span>⁻⁵F且C2=10⁻⁹F时,我们可以得到如图7所示的特性。

图7:包络检波器(方波)
